Question

Samuel tosses a football from the top of a hill. The football's height h, in feet, after t seconds is modeled by the equation h = −16t2 + 16t + 12. After how many seconds will the football reach the ground?

Answer 1

In this question it is given that Samuel tosses a football from the top of a hill. The football's height h, in feet, after t seconds is modeled by the equation

`h = -16t^2 +16t+12`

When football reach the ground, then value of h is 0 .

So we have to put 0 for h and solve for t. That is

`-16t^2 +16t+12=0`

`16t^2 -16t-12=0`

`4(4t^2 -4t-3)=0`

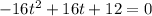
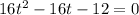
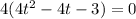
Dividing both sides by 4 to get rid of 4

`4t^2 -4t-3=0`

`(2t-3)(2t+1)=0`

`2t-3=0 , 2t+1=0`

`t=3/2 , t=-1/2`

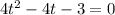
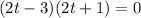
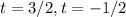
And time cant be negative. SO the time by which football reach the ground is 3/2 or 1.5 seconds .