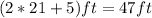Question

A rectangular garden is 5 feet longer than twice its width. It has a sidewalk 3 feet wide on two of its sides. The area of the sidewalk is 213 square feet. Find the dimensions of the garden.

Answer 1

The length and width of the garden are 47 ft and 21 ft respectively.

Step-by-step explanation

Suppose, the width of the garden is
`x` feet.

As the garden is 5 feet longer than twice its width, so the length will be:
`(2x+5) feet`

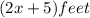
So, the area of the garden
`= length*width=x(2x+5)ft^2`

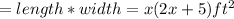
Now, the garden has a sidewalk 3 feet wide on two of its sides. That means, the length of the garden including the sidewalk
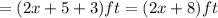`=(2x+5+3)ft =(2x+8)ft` and the width including the sidewalk
`=(x+3)ft`

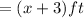
Given that, the area of the sidewalk is 213 ft². So the equation will be.....

`(2x+8)(x+3)-x(2x+5)=213\\ \\ 2x^2+14x+24-2x^2-5x=213\\ \\ 9x+24=213\\ \\ 9x=189\\ \\ x=(189)/(9)=21`

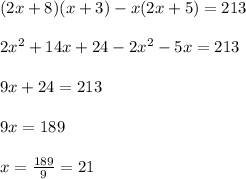
So, the width of the garden is 21 feet and the length is
`(2*21+5)ft= 47 ft`