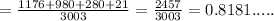Question

Involving the selection of frozen dinners. Assume that there are 15 frozen dinners: 7 pasta, 6 chicken, and 2 seafood dinners. The student selects 5 of them. What is the probability that at least 2 of the dinners selected are pasta dinners?

Answer 1

The probability that at least 2 of the dinners selected are pasta dinners will be 0.8181...

Step-by-step explanation

Pasta dinners = 7 , Chicken dinners = 6 and Seafood dinners = 2

The student selects 5 of the total 15 dinners. So, total possible ways for selecting 5 dinners
`=^1^5C_(5) =3003`

For selecting at least 2 of them as pasta dinners, the student can select 2, 3, 4 and 5 pasta dinners from total 7 pasta dinners.

So, the possible ways for selecting 2 pasta dinners
`=^7C_(2)*^8C_(3) =1176`

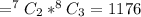
The possible ways for selecting 3 pasta dinners
`=^7C_(3)*^8C_(2) =980`

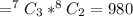
The possible ways for selecting 4 pasta dinners
`=^7C_(4)*^8C_(1) =280`

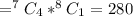
The possible ways for selecting 5 pasta dinners
`=^7C_(5)*^8C_(0) =21`

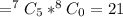
Thus, the probability for selecting at least 2 pasta dinners
`=(1176+980+280+21)/(3003) =(2457)/(3003) =0.8181.....`