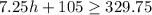Question

Sara earned $7.25 per hour plus an additional $105 in tips waiting tables last week. She earned at least $329.75. If h represents the minimum number of hours that sara could have worked, which inequality represents all the possible values of h?

Answer 1

Answer:7.25h + 105 ≥ 329.75

Step-by-step explanation:7.25h represents $7.25 multiplied by the number of h hours, and 105 represents a fixed amount of $105 in tips.

Setting the expression 7.25h + 105 greater than 329.75 allows you find all the possible values of h hours.

7.25h + 105 ≥ 329.75

7.25h ≥ 224.75

h ≥ 31

Answer 2

Given:

h represents the minimum number of hours that Sara could have worked.

Sara earned $7.25 per hour plus an additional $105 in tips waiting tables last week

She earned at least $329.75.

Solution:

We need to write an expression to represent what Sara earned in a week.

`Sara \; Earning \\= Number \; of \; hours \; she \; worked * Earnings \; per \; hour + Tips`

`Sara \; Earning = h * 7.25 + 105=7.25h+105`

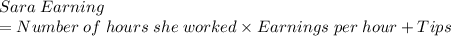
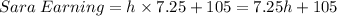
Then we need to set up an inequality given that "She earned at least $329.75"

`7.25h+105\geq 329.75`

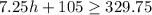
Solving the inequality by undoing whatever is done to h by performing the reverse operation as given below:

`7.25h+105\geq 329.75\\Step \; 1: Subtract \; 105 \; on \; both \; sides\\\\7.25h+105-105\geq 329.75-105\\Step \; 2: Combine \; like \; terms \; on \; both \; sides\\\\7.25h\geq 224.75\\Step \; 3: Divide \; 7.25 \; on \; both \; sides\\\\(7.25h)/(7.25)\geq (224.75)/(7.25)\\Step \; 4: Simplify \; fractions \; both \; sides\\\\h\geq 31`

Conclusion:

The inequality represents all the possible values of h is given below:

`7.25h+105\geq 329.75`