Question

I need help with this ASAP and can you explain so i can understand?!

Answer 1

Adult tickets sold = 225

Student Tickets sold = 375

Explanation:

Let:

Adult tickets sold = x

Student Tickets sold = y

Total tickets sold = 600

So, we can write: x+y = 600

Total money collected = 3037.50

Cost of 1 Adult ticket = $6.00

Cost of one Student ticket = $4.50

So, we can write: 6x+4.5y=3037.50

Now, we get a system of equations, that if solved we can find values of x and y

Let:

`x+y = 600--eq(1)\\6x+4.5y=3037.50--eq(2)`

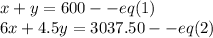
We can solve using substitution method.

Finding value of x from eq(1) and putting it in eq(2)

`We\:have\\x+y=600\\x=600-y`

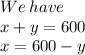
Put in eq(2)

`6x+4.5y=3037.50\\6(600-y)+4.5y=3037.50\\3600-6y+4.5y=3037.50\\-1.5y=3037.50-3600\\-1.5y=-562.5\\y=(-562.5)/(-1.5)\\y=375`

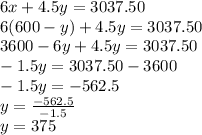
So, we get value of y = 375

Now put value of y in eq(1) to find value of x

`x+y=600\\Put\:y=375\\x+375=600\\x=600-375\\x=225`

So, we get value of x = 225

The Tickets sold will be:

Adult tickets sold = x = 225

Student Tickets sold = y = 375