Question

25
`25^(x) =(1)/(125)`

Answer 1

Given equation :
`25(25)^x = (1)/(125)`

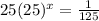
Soltution: First we need to get rid 25 in front on left side.

25 is being multiplied by (25)^x.

We need to to apply reverse operation of multiplication, that is division.

Dividing both sides by 25, we get

`(25(25)^x)/(25)=( (1)/(125))/(25)`

`(25)^x = (1)/(125*25)=(1)/(3125)`

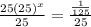
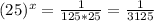
Converting 25 into exponent (power) of 5 and 3125 into exponent (power) of 5.

25=5*5= (5)^2

3125= 5*5*5*5*5 or (5)^5.

Replacing 3125 by (5)^5 on right side and 25 by (5)^2 on left side.

`((5)^2)^x=(1)/(5^5)`

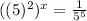
Applying negative exponent rule on rigth side
`(1)/(a^n)=a^(-n)`

`(5)^(2x)=(5)^(-5)`

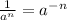
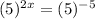
Comparing exponent on both sides, we get

2x=-5

Dividing both sides by 2, we get

2x/2 = -5/2

x=-5/2