Question

I really need help , im so confused .I need someone to go over it with me . Prove the polynomial identity. (a−1)^3+(a−1)^2=a(a−1)^2 Drag and drop the expressions to correctly complete the proof of the polynomial identity. The options and blank spaces they give me are in the attachements

Answer 1

Given:
`(a-1)^3+(a-1)^2=a(a-1)^2`

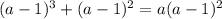
Step 1) Expanding (a-1)^3 by using difference of the cube formula

We know,
`(x-y)^2= x^3 - y^3 -3x^2y+3xy^2`.

Therefore,
`(a-1)^3 = (a)^3-(1)^2 -3(a)^2(1) +3(x)(1)^2=a^3 -1 -3a^2 +3x`

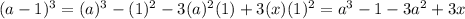
Now, expanding (a-1)^2 by using formula of (x-y)^2

`(x-y)^2= x^2 - 2xy + y^2.`

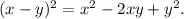
Therefore,

`(a-1)^2 = a^2-2a + 1`

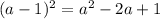
On the left side we get

a^3-3a^2+3a-1+a^2-2a + 1 ( Please put this expression in first box)

Step 2) Combining like terms,

a^3-2a^2+a ( Please put this expression in second box)

Step 3) Factoring out gcf a, we get

a (a^2-2a+1) ( Please put this expression in third box)

Step 4)

Factoring out a^2 -2a+1, (a-1)(a-1).

a(a-1)(a-1) ( Please put this expression in fourth box)

(a-1)(a-1) equals (a-1)^2 because (a-1) is two times there.

Finally, we are given a(a-1)^2 = a(a-1)^2 in last expression on the board.