For multiplying two polynomials, we will multiply each term in the first parenthesis with the whole second parenthesis part and then use distributive property and simplify in the end.
Polynomial product A
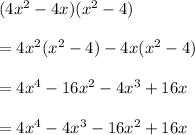
Polynomial product B
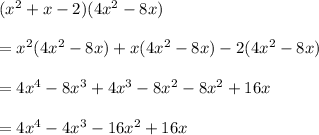
Thus, the products of the two polynomials are the same.