Question

If the spring constant is doubled, what value does the period have for a mass on a spring? A. The period would double by square `sqrt(2)`. B. The period would be halved by `sqrt(2)`. C. The period would increase by `sqrt(2)`. D. The period would decrease by `sqrt(2)`.

Answer 1

Answer D. is INCORRECT on PLATO!!!!

Step-by-step explanation:

Answer 2

The period would decrease by sqrt(2)

Step-by-step explanation:

The restoring force is given by,

F = -kx

According to Newton's second law of motion,

ma = -kx

ma + kx = 0

The time period is given by,

T =
`(2\pi )/(\omega )`

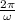
Where
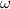`\omega` is the angular velocity and it is given by,

`\omega` =
`\sqrt{(k)/(m) }`

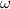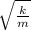
Now if the spring constant is doubled then,

`k_(2) = 2k`

Thus,

`T_(2)` =
`\frac{2\pi }{\sqrt{(2k)/(m) } }`

`(T_(2) )/(T) = \frac{\frac{2\pi }{\sqrt{(2k)/(m) } }}{\frac{2\pi }{\sqrt{(k)/(m) } }}`

`(T_(2) )/(T) = \sqrt{(k)/(2k) } = \sqrt{(1)/(2) }`

`T_(2) = (T)/(√(2) )`

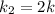
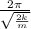
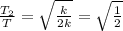
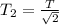
Thus, The period would decrease by sqrt(2).

Hence, option D is correct.