Question

Determime the intercepts of the line that passes through the following points. (-6,5);(-3,3);(0,1)

Answer 1

well for a line, to get its slope all we need is two points, so let's use (-6, 5) and (0, 1), and get the equation of it.

`\bf (\stackrel{x_1}{-6}~,~\stackrel{y_1}{5})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{1}) \\\\\\ slope = m\implies \cfrac{\stackrel{rise}{ y_2- y_1}}{\stackrel{run}{ x_2- x_1}}\implies \cfrac{1-5}{0-(-6)}\implies \cfrac{1-5}{0+6}\implies -\cfrac{5}{6}`

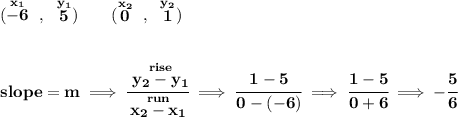
`\bf \begin{array}ll \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-5=-\cfrac{5}{6}[x-(-6)]\implies y-5=-\cfrac{5}{6}(x+6) \\\\[-0.35em] \rule{34em}{0.25pt}\\\\ \textit{to get the x-intercept, we set y = 0, solve for \underline{x}} \\\\\\ 0-5=-\cfrac{5}{6}(x+6)\implies -30=5x+30\implies -60=5x \\\\\\ \cfrac{-60}{5}=x\implies -12=x~\hfill \boxed{\stackrel{x-intercept}{(-12,0)}}`

now, where's the y-intercept of that line? well, to get the y-intercept, we set x = 0 and solve for "y"....hmmmm wait a second, notice (0, 1), x = 0, y = 1, that's the y-intercept already.