The inverse function of the logarithm is the exponential function:

In fact, the expression
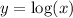 means that if you want to obtain x, you have to give y as exponent to e:
means that if you want to obtain x, you have to give y as exponent to e:
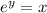
So, we can check both expressions:
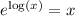 , because this expression means "I am giving to e the following exponent: a number that, when given as exponent to e, gives x".
, because this expression means "I am giving to e the following exponent: a number that, when given as exponent to e, gives x".
On the other hand, you have
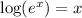 , because this expression means "what exponent do I have to give to e to obtain e^x?". Well, you've basically already written it: if you want to obtain e^x, you have to give the exponent x.
, because this expression means "what exponent do I have to give to e to obtain e^x?". Well, you've basically already written it: if you want to obtain e^x, you have to give the exponent x.
So, we've shown that
 , which proves that
, which proves that
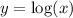 and
and
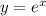 are one the inverse function of the other.
are one the inverse function of the other.