Question

Identify whether the series summation of 12 open parentheses 3 over 5 close parentheses to the i minus 1 power from 1 to infinity is a convergent or divergent geometric series and find the sum, if possible.Identify whether the series summation of 12 open parentheses 3 over 5 close parentheses to the i minus 1 power from 1 to infinity is a convergent or divergent geometric series and find the sum, if possible.

Answer 1

Given series is sigma i=1 to infinity 12*
`(3)/(5) ^(i-1)`,

=
`12+ 12*(3)/(5) + 12*(3)/(5)^(2)+.......`

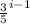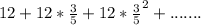
Clearly it is a geometric series and it converges if and only if r<1

So, common ratio =
`(3)/(5)` < 1

Hence the series is convergent.

Formula for sum of infinite geometric series =
`(a)/(1-r)`

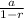
Where a is the first term and r is the common ratio.

So, sum of series =
`(12)/(1-(3)/(5) ) = (12)/((2)/(5) )`

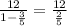
For taking 2/5 to numerator we have to multiply with reciprocal 5/2 on both numerator and denominator.

Hence sum of series = 12*
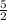`(5)/(2)` = 30