Question

Why is the product of a rational number and an irrational number irrational

Answer 1

A proof by contradiction.

Let assume that the product of a rational number and an irrational number is rational.

Let
`(a)/(b)` and
`(c)/(d)` be rational numbers, where
`a,b,c,d\in \mathbb{Z} \wedge b,d\\ot=0` and
`x` an irrational number.

Then

`(a)/(b)\cdot x=(c)/(d)\\ x=(bc)/(ad)`

Integers are closed under multiplication, therefore
`bc` and
`ad` are integers, making the number
`x=(bc)/(ad)` rational, which is contradictory with the earlier statement that
`x` is an irrational number.

Answer 2

Great question. Let's let r be a rational number and s be irrational. Note r has to be nonzero for this to work. In other words, it's not true that when we multiply zero, a rational number, by an irrational number like π we get an irrational number. We of course get zero.

The question is: why is the product

`p = rs`

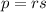
irrational?

In math "why" questions are usually answered with an illuminating proof. Here the indirect proof is enlightening.

Suppose p was rational. Then

`s = \frac p r`

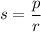
would be rational as well, being the ratio of two rational numbers, so ultimately the ratio of two integers.

But we're given that s is irrational so we have our contradiction and must conclude our assumption that p is rational is false, that is, we conclude p is irrational.