Solution: We are given that the time spent on tumblr, a microblogging platform and social networking website is normally distributed with mean = 14 minutes and standard deviation = 4 minutes
We have to find, If we select a random sample of 25 visits, the probability that the sample mean is between 13.6 and 14.4 minutes. In other words, we have to find:

First we have to find the z scores as:


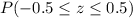
Using the standard normal table, we have:
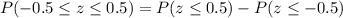
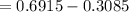
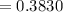
Therefore, if a random sample of 25 visits is selected, the probability that the sample mean is between 13.6 and 14.4 minutes is 0.3830