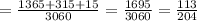Question

Suppose a box contains 3 defective light bulbs and 15 good bulbs. Four bulbs are chosen from the box without replacement.

a. Find the probability that one of the bulbs drawn is good.
b. Find the probability that none of the bulbs drawn are defective.
c. Find the probability that at least one of the bulbs drawn are defective.

Answer 1

Number of defective light bulbs = 3 and number of good bulbs = 15

So, there are total (3+15) or 18 bulbs in the box.

4 bulbs are chosen from the box without replacement. So, the number of ways for choosing 4 bulbs from total 18 bulbs
`= ^1^8C_(4)=3060`

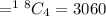
a. One of the bulbs drawn is good means 1 bulb is chosen from 15 good bulbs and remaining 3 bulbs are chosen from 3 defective bulbs. So, the possible number of ways
`= ^1^5C_(1)*^3C_(3) = 15`

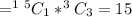
Thus, the probability that one of the bulbs drawn is good
`=(15)/(3060)=(1)/(204)`

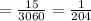
b. None of the bulbs drawn are defective means 4 bulbs are chosen from 15 good bulbs. So, the possible number of ways
`=^1^5C_(4)= 1365`

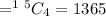
Thus, the probability that none of the bulbs drawn are defective
`= (1365)/(3060)=(91)/(204)`

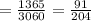
c. At least one of the bulbs drawn are defective means number of defective bulbs can be 1 or 2 or 3.

If 1 bulb is chosen as defective, then the number of ways
`=^3C_(1)*^1^5C_(3) = 1365`

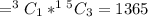
If 2 bulbs are chosen as defective, then the number of ways
`=^3C_(2)*^1^5C_(2) = 315`

and if 3 bulbs are chosen as defective, then the number of ways
`=^3C_(3)*^1^5C_(1) = 15`

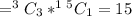
Thus, the probability that at least one of the bulbs drawn are defective
`=(1365+315+15)/(3060)=(1695)/(3060)=(113)/(204)`