Question

Please help me understand

Answer 1

x=4

y=6

Explanation:

We need to find value of x and y if RS bisects AB and RS = 28

We are given: RS = 28

and We can see from figure that: RT= 3y-7 and TS = 2y+5

And we can observe that RT + TS = 36

So, putting all the values, we can find value of y

`3y-7+2y+5=28`

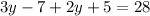
Solving this equation, will find value of y

`3y+2y+5-7=28\\5y-2=28\\5y=28+2\\5y=30\\y=(30)/(5)\\y=6`

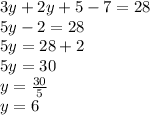
So, we get value of y: y=6

Now, we also know that RS bisects the line AB. It means it divides both the lines equally.

So, we can write: AT = TB

Putting values we can find value of x

We have AT = 4x-2

TB = 4y+2

and y =6

`4x-2 = 4y+2\\4x-2=4(6)+2\\4x-2=12+2\\4x=14+2\\4x=16\\x=(16)/(4)\\x=4`

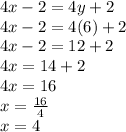
So, we get value of x: x=4