Question

A certain element x has four isotopes. 4.350% of x has a mass of 49.94605 amu. 83.79% of x has a mass of 51.94051 amu. 9.500% of x has a mass of 52.94065 amu. 2.360% of x has a mass of 53.93888 amu. What is the average atomic mass of element x? Express your answer numerically to four significant figures. View available hint(s)

Answer 1

Answer: 52.00 amu.

Explanation:

Mass of isotope 1 = 49.94605 amu

% abundance of isotope 1 = 4.350% =
`(4.350)/(100)=0.0435`

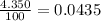
Mass of isotope 2 = 51.94051 amu

% abundance of isotope 2 = 83.79 % =
`(83.79)/(100)=0.8379`

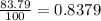
Mass of isotope 3 = 52.94065 amu

% abundance of isotope 3 = 9.500 % =
`(9.500)/(100)=0.095`

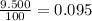
Mass of isotope 4 = 53.93888 amu

% abundance of isotope 4 = 2.360 % =
`(2.360)/(100)=0.0236`

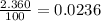
Formula used for average atomic mass of an element :

`\text{ Average atomic mass of an element}=\sum(\text{atomic mass of an isotopes}* {{\text { fractional abundance}})`

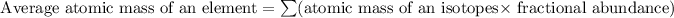
`A=\sum[(49.94605* 0.0435)+(51.94051* 0.8379)+(52.94065* 0.095)+(53.93888* 0.0236)]`

`A=52.00amu`

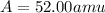
Therefore, the average atomic mass of an element is 52.00 amu.

Answer 2

Average atomic mass of an element is the sum of atomic mass of its isotopes multiplied by their respective percentage abundance.

There are four isotopes of element X:

1. 4.350 % with mass 49.94605 amu

2. 83.79% with mass 51.94051 amu

3. 9.5% with mass 52.94065 amu

4. 2.360% with mass 53.93888 amu

Thus, average atomic mass will be:

`=49.94605((4.350)/(100))+51.94051((83.79)/(100))+52.95065((9.5)/(100))+53.93888((2.360)/(100))`

Or,

`Average atomic mass=2.173 amu+43.52 amu+5.029 amu+1.273 amu=51.99 amu`

Therefore, average atomic mass of element X will be 51.99 amu (four significant figures)