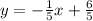Question

"find the equation of the line passing through the point (1,1) and perpendicular to the line y=5x-1 enter the exact answer. Use improper fractions if it is necessary, do not use mixed fractions."

Answer 1

The equation of the perpendicular line will be:
`y=-(1)/(5)x+(6)/(5)`

Step-by-step explanation

Given equation of the line :
`y= 5x-1`

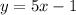
After comparing the above equation with slope intercept form
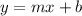`y= mx+b`, we will get: Slope
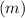`(m)` = 5

As the slope of a perpendicular line is negative reciprocal of the slope of given line, so here the slope of the perpendicular line will be:
`-(1)/(5)`

Now, the perpendicular line have slope
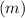`(m)` as
`-(1)/(5)` and it's passing through the point
`(x_(1), y_(1))` =
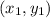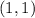`(1,1)` , so using the point-slope form......

`y- y_(1)= m(x-x_(1))\\ \\ y-1= -(1)/(5)(x-1)\\ \\ y-1= -(1)/(5)x+(1)/(5)\\ \\ y= -(1)/(5)x+(1)/(5)+1\\ \\ y=-(1)/(5)x+(6)/(5)`

So, the equation of the perpendicular line will be:
`y=-(1)/(5)x+(6)/(5)`

Answer 2

In this question, we have o find the equation of line passing through point (1,1) and is perpendicular to the line

`y = 5 x-1`

And slope of the given line is 5. And slopes of perpendicular lines are opposite and reciprocal of each other.

So slope of perpendicular line is

`m = - (1)/(5)`

Using slope intercept form, which is

`y=mx+b`

Substituting the values of x and y from the given point, and the value of m, we will get

`1= -  (1)/(5) +b`

adding 1/5 to both sides

`1 + (1)/(5) = b \\ b = (6)/(5)`

So the required equation of line is

`y = - (1)/(5) x + (6)/(5)`