Question

A 3-mi cab ride costs $7.30. A 8-mi cab ride costs $15.30. Find a linear equation that models a relationship between cost c and distance d.

Select one:
a. c = 1.91d + 2.50
b. d = 1.60c + 8.00
c. c = 1.60d + 2.50
d. c = 2.43d + 8.00

Answer 1

Since, A 3-mi cab ride costs $7.30 and a 8-mi cab ride costs $15.30.

In the information given above, we can consider these as the coordinate points on the axes.

Let (c, d) be the coordinates , where 'c' represents the total cost and 'd' represents the distance traveled.

Cost is on the 'y' axis and distance is on the 'x' axis.

Now, let the first point on the coordinate axes be (3, 7.30) and the other point is given by (8, 15.30).

For the given points say
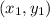`(x_1,y_1)` and
`(x_2,y_2)` , equation of line is given by:

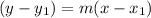`(y-y_1)= m(x-x_1)` where m(slope) is given by
`(y_2-y_1)/(x_2-x_1)`.

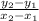The equation of line for the given points is:

`(c-7.30) = ((15.30-7.30)/(8-3))(d-3)`

`(c-7.30) = 1.6(d-3)`

`c-7.30 = 1.6d-4.8`

`c-1.6d=2.5`

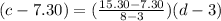
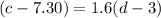
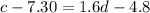
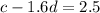
So, c = 1.6d+2.5 is the required linear equation that models a relationship between cost c and distance d.