The given limit is
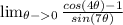
If we put 0 for theta , we will get 0/0 , which is not defined.
SO in this case we use L- Hospital's rule and differentiate both numerator and denominator. That is
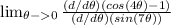
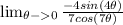
Using substitution property of limit
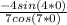

Therefore the value of the limit is 0.