Question

A flat circular plate of copper has a radius of 0.379 m and a mass of 71.4 kg. what is the thickness of the plate? answer in units of m.

Answer 1

We use the formula,

`m = V * \rho`.

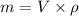Here, m is mass, V is the volume and
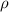`\rho` is density.

We can also write above equation as,

`m = \pi r ^2  t * \rho`.

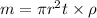Here,
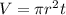`V = \pi r ^2  t`, t is thickness circular plate of copper.

Given
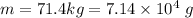`m = 71.4 kg = 7.14 * 10^4 \ g` and
`r = 0.379 m = 37 .9 cm`.

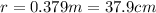The density of copper = 8.94 g/ cm³.

Substituting these values in above formula we get,

`7.14 * 10^4 \ g = 3.14 * (37 .9 cm)^2 *  t * 8.94 \ g/ cm^3 \\\\ t = (7.14 * 10^4 \ g)/( 4.0 * 10^4 g / cm) \\\\\ = 1.78 \ cm = 1.78 * 10^(-2) m`.

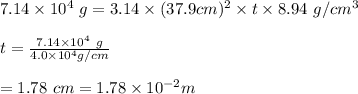Thus, the thickness of the plate is 0.0178 m.