Question

Given that ∠A and ∠B are supplementary, Daisy conjectured that ∠A≅∠B . Which statement is a counterexample to Daisy's conjecture?

A. m∠A=50° and m∠B=120°

B. m∠A=45° and m∠B=45°

C. m∠A=40° and m∠B=140°

D. m∠A=90° and m∠B=90°

Answer 1

I believe the answer is C. 40 and 140.

Answer 2

C. m∠A=40° and m∠B=140°

Explanation:

We have been given that ∠A and ∠B are supplementary, Daisy conjectured that ∠A≅∠B. We are asked to find the counterexample to Daisy's conjecture.

We know that a counterexample is an example that contradicts an idea or theory.

Since ∠A and ∠B are supplementary, so they will add up-to 180 degrees.

`\angle A+\angle B=180^(\circ)`

Daisy conjectured that ∠A≅∠B, so the measure of angle A will be equal to measure of angle B.

`m\angle A=m\angle B`

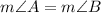
This means that measure of angle A and B is 90 degrees.

The counterexample to Daisy's conjecture would be example that shows the measure of angle A and measure of angle B other than 90 degrees.

Upon looking at our given choices, we can see that option C shows that measure of angle A is 40 degrees and measure of angle B is 140 degrees, therefore, option C is a counterexample to Daisy's conjecture.