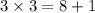Question

I've attempted to solve this problem, but I keep getting inncorect values. Can someone help explain what I'm doing incorrectly and give me the correct values? (Algebra 2)

Answer 1

Call the three numbers
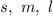`s,\ m,\ l` (small, medium and large).

Their sum is 16, so we have

`s+m+l=16`

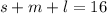
The largest is the sum of the other two, so we have

`s+m=l \iff s+m-l=0`

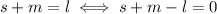
Finally, we know that three times the smaller (3s) is one less than the largest (l+1), so we have

`3s = l+1 \iff 3s-l = 1`

So, we have the following system:

Subtract the second equation from the first:

`(s+m+l) - (s+m-l) = 16-0 \iff 2l = 16 \iff l = 8`

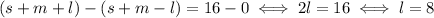
Use this value for
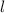`l` in the third equation to find
`s`:

`3s-l = 1 \iff 3s - 8 = 1 \iff 3s = 9 \iff s = 3`

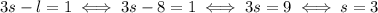
We know that the largest is the sum of the other two, so we have

`s+m=l \iff 3+m=8 \iff m=5`

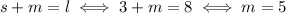
So, the three numbers are 3, 5 and 8. You can check that they have all the required features:

• Their sum is 16:
  `3+5+8=16`
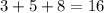
• The largest is the sum of the other two:
  `8 = 3+5`
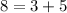
• Three times the smaller is one more than the largest:
  `3* 3 = 8+1`