I'll try to detail as much as possible the solution to exercise 2. Exercises 4 and 5 and basically identical: you'll have to set up a system translating the sentences to equations, and solve it. Please try to solve exercises 4 and 5 on your own (that's when you really learn!!) by mimicking how I solved exercise 2.
Let's call the three angles
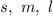 (small, medium and large, respectively). The first sentence translates to
(small, medium and large, respectively). The first sentence translates to

The second sentence translates to
Since we have three unknowns, we need a third equation: this equation is implicit, because we know that the sum of the angles of a triangle is always 180 degrees:

So, we have the following system (rearranged in standard form):

If you subtract the first equation from the third you get
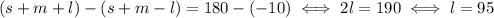
Plug this value for
 in the second equation:
in the second equation:
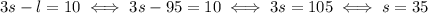
Finally, complete to 180 to compute
 :
:
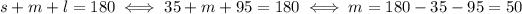
So, the angles are 35, 50 and 95 degrees