Question

The relationship between the radius, r, of a sphere and its volume, v, us r = ( 3v / 4 • pi ) 1/3. What is the radius of a sphere that has a volume of 36 pi cubic units

Answer 1

Since volume of a sphere(V) =
`(4 \pi r^3)/(3)`

V =
`(4 \pi r^3)/(3)`

`r =( {(3V)/(4 \pi)})^ (1)/(3)`

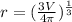
So, the relationship between the radius and volume of sphere is given by
`r =( {(3V)/(4 \pi)})^ (1)/(3)`.

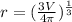Now, it is given that the volume of sphere is
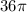`36 \pi` cubic units. we have to determine the radius of the sphere.

`r =( {(3 * 36 \pi)/(4 \pi)})^ (1)/(3)`

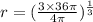
Cancelling
`\pi` from numerator and denominator, we get

`r =( {(3 * 36)/(4)})^ (1)/(3)`

`r =( {{3 * 9})^ (1)/(3)`

`r =( {27})^ (1)/(3)`

`r =( {3^3})^ (1)/(3)`

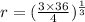
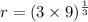
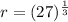
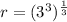
So, r = 3 units

Therefore, the radius of the sphere is 3 units.