Question

A theater has a seating capacity of 750 and charges $5 for children, $7 for students, and $9 for adults. At a certain screening with full attendance, there were half as many adults as children and students combined. The receipts totaled $4950. How many children attended the show

Answer 1

Let 'c' be the number of children, 'a' be the number of adults and 's' be the number of students in the theater.

Since, there are total 750 people in the theater.

So, c + s + a = 750 (Equation 1)

Now, it is given that there were half as many adults as children and students combined.

So,
`a= (c+s)/(2)`

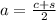
So,
`c+s = 2a`

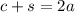
Putting the value of "c+s" in equation 1.

`c+s+a=750`

`2a+a = 750`

`3a= 750`

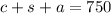
a = 250

Now, it is given that the receipts totaled $4950 and it charges $5 for children, $7 for students, and $9 for adults.

So,
`( 5 * c) +( 7 * s )+ (9 * a) = \$4950` (equation 2)

Since,
`c+s = 2a`

`c+s = 500`

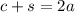
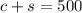
So,
`s = 500-c`

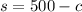
Substituting the values of 's' and 'a' in equation 2, we get

`5c+7s+9a= 4950`

`5c+ 7(500-c)+(9 * 250) = 4950`

`5c+3500-7c+2250=4950`

`-2c= -800`

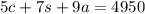
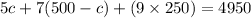
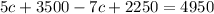
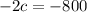
So, c = 400

Therefore, there were 400 children at the theater.