Consider the given equations:
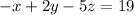 (Equation 1)
(Equation 1)
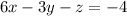 (Equation 2)
(Equation 2)
 (Equation 3)
(Equation 3)
Adding equations 1 and 3, we get

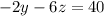
So, we get
 (Equation 4)
(Equation 4)
Multiplying equation 3 by '6', we get
 (Equation 5)
(Equation 5)
Subtracting equation 5 from equation 2, we get

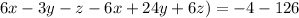
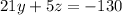 (Equation 6)
(Equation 6)
Multiplying equation 4 by '21' and adding it to equation 6, we get
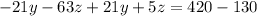
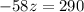
So, z = -5
Since,

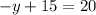
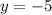
So, y=-5
Now,


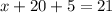
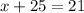
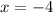
So, x = -4
Therefore, x = -4, y= -5 and z= -5 are the solutions to the given equations.