Question

Direct and inverse variation

Answer 1

4 workers can do the job in 18 days.

Explanation:

The number of days d varies inversely as the number of workers.

We can write it as:
`d\: \alpha\: (1)/(w) \\d=(k)/(w)`

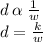
where k is constant of proportionality

We are given: If it takes 9 days for 8 workers to complete the job, then how many workers would it take to do the job in 18 days.

d = 9, w = 8

d = 18, w =?

First we will find value of k when d = 9, w =8

`d=(k)/(w)\\9=(k)/(8)\\k=9*8\\k=72`

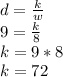
The value of k, will remain same as it is constant.

We get k = 72.

So, Now we have d = 18, k = 72 and we need to find w

`d=(k)/(w)\\18=(72)/(w)\\18w=72\\w=(72)/(18)\\w=4`

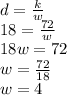
So, 4 workers can do the job in 18 days.