Question

The midpoint of UV is (5, -10). The coordinates of one endpoint are U(3,6). Find the coordinates of endpoint V.

How do I use the midpoint formula for this?

Answer 1

The coordinates of point V is (7,-26)

Explanation:

Let W be the midpoint of line UV

So, Coordinates of W = (x,y) = (5,-10)

We are given that coordinates of point U are
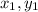`x_(1),y_(1)` =(3,6)

Now to find the coordinates of point V denoted by
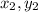`x_(2),y_(2 )` , we will use mid point formula since UV is the line and W is its midpoint .

Formula of midpoint :

`(x,y)=((x_(1)+x_(2) )/(2) ,(y_(1) +y_(2) )/(2) )`

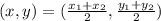
Now putting values in the formula we will get :

`(5,-10)=((3+x_(2) )/(2) ,(6+y_(2) )/(2) )`

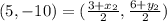
Thus
`x= (x_(1)+x_(2) )/(2)`

⇒
`5 = (3+x_(2) )/(2)`

⇒
`5 *2 = 3+x_(2)`

⇒
`10 = 3+x_(2)`

⇒
`10 - 3 = x_(2)`

⇒
`7 = x_(2)`

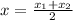
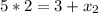
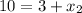
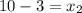
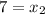
Now,
`y = (y_(1) +y_(2) )/(2)`

⇒
`-10 = (6 +y_(2) )/(2)`

⇒
`-10*2 = 6 +y_(2)`

⇒
`-20 = 6 +y_(2)`

⇒
`-20 - 6 = y_(2)`

⇒
`-26 = y_(2)`

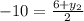
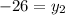
Thus,
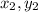`x_(2),y_(2 )` =(7,-26)

Hence ,The coordinates of point V is (7,-26)

Answer 2

The answer is (7, -26) for The second endpoint.

We'll call the midpoint M. In order to find this, we must first note that to find a midpoint we need to take the average of the endpoints. To do this we add them together and then divide by 2. So, using that, we can write a formula and solve for each part of the k coordinates. We'll start with just x values.

(Ux + Vx)/2 = Mx

(Vx + 3)/2 = 5

Vx + 3 = 10

Vx = 7

And now we do the same thing for y values

(Uy + Vy)/2 = My

(Vy + 6)/2 = -10

Vy + 6 = -20

Vy = -26

This gives us the final point of (7, -26)