Given equation: A(n - 3) +8= bn.
Solution: On the left side of the equation we have A(n-3).
We don't have any sign in between A and parenthesis (n-3).
So, we need to multiply A and (n-3).
We need to apply distributive property to multiply A and (n-3).
Distributing A over (n-3), we get
A(n-3) = A*n - 3*A = An -3A.
Substituting this value in original equation,
An -3A +8= bn.
We need to solve it for n, so we get n terms on a side.
We have An on left side, we need to get rid n from left side.
Subtracting An from both sides, we get
An -3A +8-An= bn-An.
-3A +8 = bn - An.
We can see n is a common factor on rigth side in bn-an.
Factoring out n on right side from bn-an.
-3A +8 = (b - A)n.
Dividing both sides by (b-A),
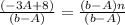
On right (b-A) paranthiss cancelled and we get n on right side.
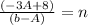 Final answer.
Final answer.
So, that would be our final answer
n = (-3A+8)/(b-A)