Answer: option A. h < 0 and k < 0
Step-by-step explanation:
1) You can obtain the graph of the function f(x)
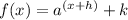
by comparing it with the parent function g(x)
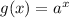
2) As you see above, in this case it is verified that f(x) = g(x + h) + k.
3) And, from the graphing rules, you can use the fact that the graph of g(x+h) + k is the graph of g(x) shifted h units to the left and k units upward.
4) The graph of
 cuts the y-axis on 1, this is the point (0,1), and its limit trends to 0⁺ when x trends to negative infinity.
cuts the y-axis on 1, this is the point (0,1), and its limit trends to 0⁺ when x trends to negative infinity.
5) Then, since, relative fo the parent function, the given graph shows a translation towards the right, h is negative, and, since it shows a translation downward, k is also negative.
In conclusion, the option A. h < 0 and k < 0, is the correct answer.