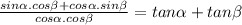Question

Complete the identity. (sin(\alpha +\beta ))/(cos\alpha cos\beta )

Answer 1

`(sin\alpha.cos\beta +cos\alpha.sin\beta)/(cos\alpha.cos\beta)=tan\alpha +tan\beta`

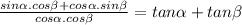
Step-by-step explanation:

Here are the steps to simplify the expression and obtain the identity.

1) Given:

`(si(\alpha+\beta))/(cos(\alpha)cos(\beta))`

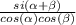
2) Use the identity sin(α + β) = sin(α)cos(β) + cos(α)sin(β)

`(sin\alpha.cos\beta +cos\alpha.sin\beta)/(cos\alpha.cos \beta)`

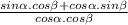
3) Distributive property of division:

`(sin\alpha.cos\beta)/(cos\alpha.cos \beta)+(cos\alpha.sin\beta)/(cos\alpha.cos \beta)`

4) Simplify common factors in numerators and denominators

`(sin\alpha)/(cos\alpha )+(sin\beta)/(cos \beta)`

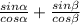
5) Definition of tangent ratio

tanα + tanβ

6) Conclusion

`(sin\alpha.cos\beta +cos\alpha.sin\beta)/(cos\alpha.cos \beta)=tan\alpha +tan\beta`