Question

Which solution to the equation 3/2g+8 g+2/g^2-16 is extraneous? A. g = –4 B. g = –4 and g = 16

C. neither g = –4 nor g = 16
D. g = 16

Answer 1

im assuming the equation is:-

3 / (2g + 8) = (g + 2) / (g^2 - 16)

3(g^2 - 16) = (2g + 8)(g + 2)

3g^2 - 48 = 2g^2 + 4g + 8g + 16

Answer is A x = -4

3g^2 - 2g^2 - 12g - 64 = 0

g^2 - 12g - 64 = 0

( g + 4)(g - 16) = 0

g = - 4, 16.

Test these solutions:-

g = -4

left side = 3/0 which is indeterminate

right side = -2/0 indeterminate

So x = -4 is extraneous.

x = 16:- LHS = 0.075 RHS = 0.075 so x = 16 is a root.

Answer 2

g = -4 is the extraneous solution.

Explanation:

The given equation :

`(3)/((2g+8))=((g+2))/((g^(2)-16))`

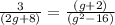
3 (g²-16) = ( g + 2 ) ( 2g + 8 )

3g² - 48 = 2g² + 8g + 4g + 16

( 3g² - 2g² ) = ( 8g + 4g ) + ( 16 + 48 )

g² = 12g + 64

g² - 12g - 64 = 0

g² - 16g + 4g - 64 = 0

g ( g- 16 ) + 4 ( g - 16 ) = 0

( g + 4 ) ( g - 16 ) = 0

Since ( g + 4 ) & ( g - 16 ) are zero factors

So, g = -4, 16

Now we test these solutions. for (g = -4)

L.H.S (Left Hand Side)=
`(3)/(2(-4)+16)=(3)/((-8+16))=-((3)/(8))`

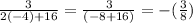
R.H.S. (Right Hand Side) =
`((g+2))/((g^(2)-16) )=(-4+2)/(16-16)=(2)/(0)`

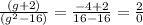
L.H.S. ≠ R.H.S. So g = ( -4) is not the answer, so g = -4 is the extraneous solution.

Now for g = 16

L.H.S.
`((3)/(32+8))=(3)/(40)`

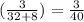
and R.H.S.
`(16+2)/(256-16)=(18)/(240)=(3)/(40)`

so LHS = RHS

Therefore. g = 16 is not the extraneous solution.