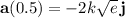Question

A particle follows a planar path defined by x = kξ, y = 2k[1 − exp(ξ )], such that its speed is v = βξ, where k and β are constants. Determine the velocity and acceleration at ξ = 0.5

Answer 1

The velocity of the particle
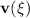`\mathbf v(\xi)` is given by the derivative of the position vector
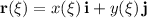`\mathbf r(\xi)=x(\xi)\,\mathbf i+y(\xi)\,\mathbf j`. We have

`\mathbf r(\xi)=k\xi\,\mathbf i+2k(1-e^\xi)\,\mathbf j`

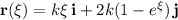
with derivative

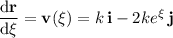
`(\mathrm d\mathbf r)/(\mathrm d\xi)=\mathbf v(\xi)=k\,\mathbf i-2ke^\xi\,\mathbf j`

At
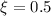`\xi=0.5`, we get a velocity vector of

`\mathbf v(0.5)=k\,\mathbf i-2k\sqrt e\,\mathbf j`

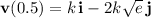
Not important as far as I can tell, but the particle's speed at
`\xi` is
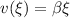`v(\xi)=\beta\xi`, which satisfies

`\|\mathbf v(0.5)\|=v(\xi)\implies√(k^2+4k^2e)=\frac\beta2`

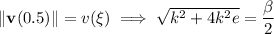
(Perhaps you may be required to solve for
`k` in terms of
`\beta`, then report the velocity/acceleration vectors with respect to
`\beta`, but I'll not do so because the original question makes no mention of needing to do that.)

Acceleration is given by the derivative of the velocity vector:

`(\mathrm d\mathbf v)/(\mathrm d\xi)=\mathbf a(\xi)=-2ke^\xi\,\mathbf j`

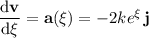
and at
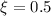`\xi=0.5`, the acceleration vector is

`\mathbf a(0.5)=-2k\sqrt e\,\mathbf j`