Question

A projectile travels in the horizontal direction at a velocity of 200 meters/second from a cliff that is 200 meters high. After how many seconds will the projectile reach the ground level?

A. 4.2 seconds

B. 6.2 seconds

C. 6.4 seconds

D. 9.2 seconds

Answer 1

The projectile's altitude at time
`t` is given by

`y=200\,\mathrm m-\frac g2t^2`

where
`g=9.8\,(\mathrm m)/(\mathrm s^2)` is the acceleration due to gravity. It reaches the ground when
`y=0`, at which point we find

`0=200\,\mathrm m-\frac12\left(9.8\,(\mathrm m)/(\mathrm s^2)\right)t^2\implies t=6.4\,\mathrm s`

so the answer is C.

Answer 2

Projectile reaches ground level after 6.4 seconds

Step-by-step explanation:

Uniformly varied rectilinear motionor also called accelerated uniform rectilinear motion, is motion characterized by having a straight line path and a constant and non-zero acceleration, therefore the speed in this motion changes uniformly depending on the direction of its acceleration.

This is what happens in this case. In this type of moving the equation used to calculate a distance traveled is:

d = Vo * t +
`(1)/(2)`*a * t²

where Vo = initial velocity, a = acceleration, d = distance traveled

In this case:

• d=200 meters
• Vo=0
• t=?

• a=gravity= 9.8
  `(m)/(s^(2) )`

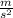
Replacing:

`200m=(1)/(2) *9.8(m)/(s^(2) ) *t^(2)`

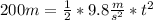
Solving for t you get:

`t=\sqrt{(200)/((1)/(2) *9.8) }`

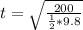
t= 6.388 seconds≅ 6.4 seconds

Projectile reaches ground level after 6.4 seconds