Question

I’ve been sitting here for hours on this specific math question, any geniuses that can solve it, I need to answer as a inequality by the way.

A number t
multiplied by −4
is at least −25

Answer 1

`\LARGE t \in (-\infty, 6.25]`

Explanation:

The inequality that represents the statement "A number t multiplied by -4is at least -25" is:

`-4t \geq -25`

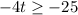
We can solve for
`t` by dividing both sides of the inequality by -4. Since we're dividing by a negative number, we need to reverse the direction of the inequality. This gives:

`t \leq (-25)/(-4)`

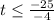
Simplifying the right-hand side, we get:

`t \leq 6.25`

Therefore, the solution to the inequality is:

`t \in (-\infty, 6.25]`

________________________________________________________

FAQ

Why did the answer have different forms of brackets? | "(" and "]"

In interval notation, we use different types of brackets to indicate whether the endpoints of an interval are included or excluded.

• A square bracket [ ] is used to indicate that an endpoint is included in the interval.

• A round bracket ( ) is used to indicate that an endpoint is not included in the interval.

Can you give me some examples?

For example, if we write the interval [0, 5], it means that the interval includes all numbers between 0 and 5, including 0 and 5. In other words, the interval includes the endpoints.

On the other hand, if we write the interval (0, 5), it means that the interval includes all numbers between 0 and 5, but does not include 0 or 5. In other words, the interval excludes the endpoints.

What about this case?

In the specific example, t ∈ (-∞, 6.25], the round bracket on the left indicates that the interval does not include negative infinity. The square bracket on the right indicates that 6.25 is included in the interval.

So, the interval includes all values of
`t` that are less than or equal to 6.25, but does not include negative infinity.

________________________________________________________

Answer 2

• given relation: -4t ≥ -25
• solution: t ≤ 25/4

Explanation:

You want an inequality that represents "A number t multiplied by −4 is at least −25".

Math symbols

The representation of the given relation using math symbols is ...

`\begin{array}{ccc}\text{a number t}&\text{multiplied by -4}&\text{is at least $-25$}\\t&(-4)&\ge-25\end{array}`

This is usually written with the coefficient in front of the variable:

-4t ≥ -25 . . . . . . . . an inequality representing the given relation

Solution

Dividing by -4 gives the solution. Multiplying or dividing by a negative number reverses the inequality symbol:

(-4t)/(-4) ≤ (-25)/(-4)

t ≤ 25/4 . . . . . as an improper fraction

t ≤ 6.25 . . . . . as a decimal number

__

Additional comment

You can see why the inequality symbol is reversed if you consider the relation between positive and negative numbers:

-2 < -1

2 > 1 . . . . . . both sides multiplied by -1

This works the same if the numbers have different signs to start:

2 > -1

-2 < 1 . . . . . both sides multiplied by -1

When an inequality is multiplied or divided by a positive number, the relationship symbol remains unchanged.

<95141404393>