We are supposed to find the distance between sun and earth of the given model, where sun's diameter is given to be 65 cm.
Let the model's distance between Earth and Sun be x.
To find the model's distance between sun and earth we can set an equation of the given information.
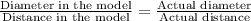
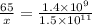
Now let us solve for x.
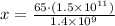
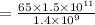
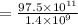
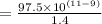
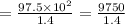
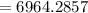
Therefore, model's distance between Earth and Sun is 6964.29 centimeters.