Question

Nicole is playing a video game where each round lasts \dfrac{7}{12} 12 7 ​ start fraction, 7, divided by, 12, end fraction of an hour. She has scheduled 3\dfrac343 4 3 ​ 3, start fraction, 3, divided by, 4, end fraction hours to play the game. How many rounds can Nicole play? rounds

Answer 1

Total number of hours she schduled to play the game = 3
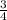`(3)/(4)` hours.

Let us convert mixed fraction into improper fraction

`3(3)/(4) = (3*3+4)/(4) = (13)/(4) \ hours.`

Duration of each round =
`(7)/(12)`.

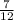In order to find the number of rounds Nicole can play, we need to divide total number of hours by duration of each round.

`(13)/(4)` ÷
`(7)/(12)`

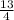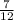
Converting division sign into multiplication flips the second fraction.

`=(13)/(4) * (12)/(7)`

Crossing out 12 by 4, we get 3 on the top of second fraction.

`=(13)/(1) * (3)/(7)`

`=(39)/(7)  = 5.57...( Approximately).`

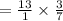
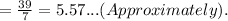
Because problem is about number of rounds.

So, total number of round would be 5.

Answer 2

Answer:it is 45/7

Explanation: