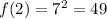For the first point, remember this simple rule: every exponential function
 always returns
always returns
 when evaluated at
when evaluated at
 . In fact,
. In fact,
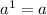 for every possible base
for every possible base
 .
.
So, we can see that the graph of the exponential passes through the point
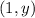 where
where
 appears to be between 1 and 2. So, the only feasible option would be
appears to be between 1 and 2. So, the only feasible option would be
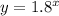 , because it passes throught the point
, because it passes throught the point
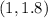 because
because
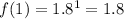 .
.
The other functions are wrong because:
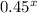 would pass through
would pass through
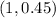 , which would be between 0 and 1 on the y axis
, which would be between 0 and 1 on the y axis
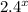 would pass through
would pass through
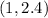 , which would be between 2 and 3 on the y axis
, which would be between 2 and 3 on the y axis
 would pass through
would pass through
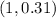 , which would be between 0 and 1 on the y axis
, which would be between 0 and 1 on the y axis
As for the second question, you simply have to plug in the values: the function
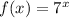
means that you have to choose an input, x, and use it as exponent for 7. So, if you choose x=2, it means that you have to give exponent 2 to 7, i.e. you replace the x with the specific value, 2.
So, the expression becomes