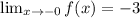Question

Suppose that f is an odd function of x. Does knowing that modifyingbelow lim with x right arrow 0 superscript plus f left parenthesis x right parenthesisequals3 tell you anything about modifyingbelow lim with x right arrow 0 superscript minus f left parenthesis x right parenthesis​? Give reasons for your answer.

Answer 1

Given f is an odd function that is f(-x) =-f(x).

And
`Lim_(x->0+)  f(x) = 3`

`Lim_(x->0-) f(x) =?`

Let x=-a

As x->0- , a->0+

So,
`Lim_(x->0-)  f(x) = Lim_(a->0+) f(-a)`

=
`Lim_(a->0+) (-f(a))` (Since f(-a)=-f(a) for odd function)

=
`-Lim_(a->0+) f(a) = -3`

Hence
`Lim_(x->0-) f(x) = -3`

Answer 2

Answer: we should have that:

`\lim_(x \to \--0) f(x) = -3`

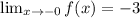
Explanation:

We know that f(x) is an odd function, this means that f(-x) = -f(x)

We know that:

`\lim_(x \to \++0) f(x) = 3`

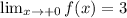
this means that wen we aproximate to zero for the right (the positive side) we have that the value is.

First, this tell us that f(x) can not be a continue function, because of the fact that is odd we will have that when we aproximate the same lim but from the negative side, we will have that:

`\lim_(x \to \--0) f(x) = -3`