First segment displacement is given as
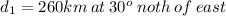
so this is given in component form as

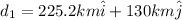
similarly the other displacement is given as
d2 = 176 km due west

now the total displacement is given as
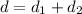
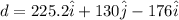
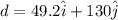
part a)
magnitude of the displacement is given as
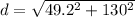
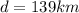
part b)
for the direction of displacement we can say
![\theta = tan^(-1)(49.2)/(130)[tex]</p><p>[tex]\theta = 20.73 degree](https://img.qammunity.org/2019/formulas/physics/high-school/hlqepdb27o9g2sdwv14eepdosikb9sprg4.png)
so it is 20.73 degree North of East