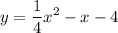Question

1.What are the distances from the point (x,y) to the focus of the parabola and the directrix?

Select two answers.

distance to the focus: √(x−2)2+(y+5)2

distance to the directrix: |y−6|

distance to the focus: √(x+4)2+(y−2)2

distance to the directrix: |x+6|

distance to the directrix: |y+6|

distance to the focus: √(x−2)2+(y+4)2

2. What is the correct standard form of the equation of the parabola?​

Answer 1

Part A)

5th and 6th Choices

Part B)

`\displaystyle y=(1)/(4)x^2-x-4`

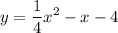
Explanation:

We are given a parabola with focus at (2, -4) and the directrix given by y = -6.

Part A)

Since our directrix is an equation of y, the distance from any point (x, y) on the parabola to the directrix will simply be the absolute value of the difference of the y-values. Hence:

`d_1=|y-(-6)|=|y+6|`

Again, we will use the distance formula. Let the point (x, y) be (x₂, y₂) and our focus (2, -4) be (x₁, y₁). Then by the distance formula:

`d_2=√((x-2)^2+(y-(-4))^2)=\sqrt{(x-2)^2+(y+4)^2`

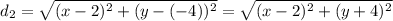
Hence, our answers are the 5th and 6th choices.

Part B)

By definition, any point (x, y) on the parabola is equidistant to the focus and the directrix. Hence:

`√((x-2)^2+(y+4)^2)=|y+6|`

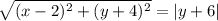
Square both sides. We may remove the absolute value as anything squared yields a positive. Hence:

`(x-2)^2+(y+4)^2=(y+6)^2`

Square:

`(x^2-4x+4)+(y^2+8y+16)=(y^2+12y+36)`

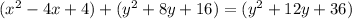
Rearrange:

`(x^2-4x+20)-(36)=(y^2-y^2)+(12y-8y)`

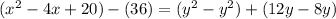
Combine like terms:

`x^2-4x-16=4y`

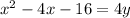
Divide both sides by 4. Hence, our equation is:

`\displaystyle y=(1)/(4)x^2-x-4`