Question

It is common to see birds of prey rising upward on thermals. The paths they take may be spiral-like. You can model the spiral motion as uniform circular motion combined with a constant upward velocity. Assume a bird completes a circle of radius 6.00 m every 5.00 s and rises vertically at a rate of 3.00 m/s. Find the angle between the bird's velocity vector and the horizontal

Answer 1

Radius of circle of spiral path = 6 m

Time period = 5 s

So the total length of the path =
`2 \pi R`

`distance = 2 \pi R`

`distance = 2 \pi *6`

`distance = 12\pi`

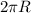
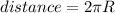
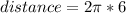
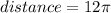
time taken by bird to cover the distance = 5 s

so the speed of the bird = distance / time

`v = (distance)/(time)`

`v = (12\pi)/(5)`

`v = 7.54 m/s`

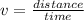
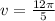
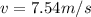
so the tangential speed in horizontal direction = 7.54 m/s

vertical velocity by which it is rising upwards = 3 m/s

so the angle with the horizontal for net speed is given as

`\theta = tan^(-1)(v_y)/(v_x)`

`\theta = tan^(-1)(3)/(7.54)`

`\theta = 21.7 degree`

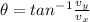
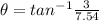
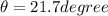
so velocity vector will make 21.7 degree with the horizontal