Question

Luigi jumps straight upwards 15.0m/s. How high is he when he is jumping at :
8.0 m/s upwards

Answer 1

Given: Initial velocity
`v_i= 15.0m/s`

Final Velocity
`v_f=8.0 m/s`

To find : Height when jumpled 8.0 m/s upwards.

Solution: We already have values of initial velocity and final velocity.

We know, accereration due to gravity is given by
`a= -9.8 m/s^2`.

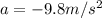It's negative because when jump it's in opposite direction.

`We know formula,  v_f ^2 = v_i ^2+2ah.`

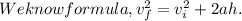
Where h is the height when jumpled 8.0 m/s upwards.

Plugging values of
`v_i, \ v_f \ and \ a \ in \ formula \ above.`

`(8.0)^2 = (15.0)^2 +2(-9.8)*h`

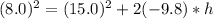
64= 225 -19.6h

Subtracting both sides by 225.

64-225= 225 -19.6h-225.

We get,

-161 = -19.6h

Dividing both sides by -19.6, we get

`(-161 )/(-19.6) =( -19.6h)/( -19.6)`

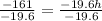
h= 8.2143

Rounding to nearest tenth, we get

h= 8.2 meter.

His height is 8.2 meter when he is jumping 8.0 m/s upwards.