Question

Wilma bought 4 boxes of Crunch-a-lot cereal. One out of every 5 boxes has a coupon for a free box of Crunch-a-Lot. What is the probability that Wilma got 2 coupons?

Answer 1

We have been given that Wilma bought 4 boxes of Crunch-a-lot cereal.

Further, we know that one out of every 5 boxes has a coupon for a free box of Crunch-a-Lot. We need to figure out the probability that Wilma got 2 coupons?

This question is based on Bernoulli's Trials. We know that probability for r successful draws out of n trials is given by:

`_(r)^(n)\textrm{C}(p)^(r)(1-p)^(n-r)`

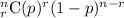
We have
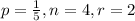`p=(1)/(5),n=4,r=2`. Upon substituting these values in this formula, we get:

`_(2)^(4)\textrm{C}((1)/(5))^(2)(1-(1)/(5))^(4-2)\\ \\ 6* ((1)/(5))^(2)((4)/(5))^(2)\\ \\ 6* (1)/(25)* (16)/(25)\\ \\ (96)/(625)\approx 0.1536`

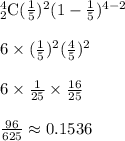
This is the required probability.