we can use
volume of cone formula
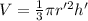
where
r' is radius of cone
h' is height of cone
we are given
The radius of the cone is half the radius of the cylinder
so,
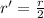
The height of the cone is equal to the radius of the cylinder
so,
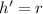
now, we can plug values into formula
we get
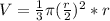
we can simplify it
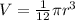
so, option-C.........Answer