Question

The amphitheater has two types of tickets available, reserved seats and lawn seats. The maximum capacity of the venue is 20,000 people. However, they must sell at least 5,000 tickets to hold a concert. As an additional constraint, the number of lawn seats cannot exceed the number of reserved seats. If reserved seats profit $65 each and lawn seats profit $40 each, how many of each seat must they sell to maximize profit?

Answer 1

Let the number of reserved tickets = x

Let the number of lawn seats = y

Constraint functions:

Maximum capacity means
`x+y\leq 20000`

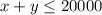
For concert to be held
`x+y\geq 5000`

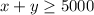
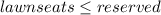`lawn seats\leq reserved` means
`y\leq x`

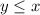
Objective functions :

Maximum profit equation p = 65x +40y

Intersection points :

(10000,10000) (20000,0)(2500,2500)(5000,0)

p at (10000,10000) = 65(10000) + 40(10000) = $1050000

p at (20000,0) = 65(20000) + 40(0) = $1300000

p at (2500,2500) = 65(2500) + 40(2500) = $262500

p at (5000,0) = 65(5000) + 40(0) = $325000

Hence maximum profit occurs when all 20000 reserved seats are sold and the profit is $1300000

Please find attached the graph of it.