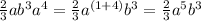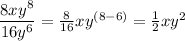In general, you make use of the rules of exponents. It can be helpful to understand where they come from.
An exponent signifies repeated multiplication.
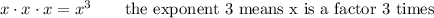
When you multiply, you add exponents.
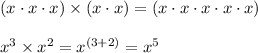
Likewise, when you divide, you subtract exponents. You can also think of this as adding the opposite of exponents that are in the denominator.
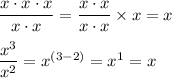
It should be no surprise then that if there are excess factors in the denominator, they can be expressed using a negative exponent.

The idea of using multiplication to show repeated addition applies to exponents as well.
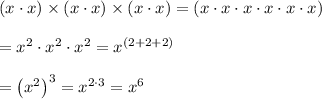
_____
With these ideas in mind ...