Question

Which values of p and q would make the value of the following expression equal to 58i? (3 – 7i)(p + qi)i

Answer 1

For short the answer is A. p = 3 , q = 7

Answer 2

we are given

`(3-7i)(p+qi)i=58i`

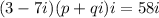
firstly, we will simplify left side

and then we can compare it with right side

so, we can distribute

`(3p+3qi-7pi-7qi^2)i=58i`

`(3p+3qi-7pi+7q)i=58i`

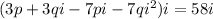
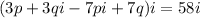
we have i on both sides

so,i will get cancelled

`(3p+3qi-7pi+7q)=58`

`(3p+7q+(3q-7p)i)=58`

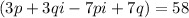
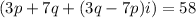
we can also write as

`(3p+7q)+(3q-7p)i=58+0*i`

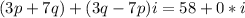
now, we can compare

and we get

`3p+7q=58`

`3q-7p=0`

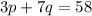
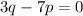
now, we can solve for p and q

we get

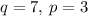`q=7,\:p=3`.............Answer