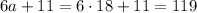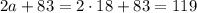The marked angles are opposite angles, and as such they have the same measure. So, we have
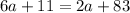
Subtract 2a and 11 from both sides to get
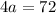
Divide both sides by 4 to get
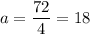
Now that we know the value of a, we can compute the measure of the angles. We can also verify that the solution we found is correct by verifying that both expressions actually give the same result: